Wartość bezwzględna, oznaczana jako |x|, jest fundamentalnym pojęciem w matematyce, definiowanym jako odległość liczby x od zera na osi liczbowej. Formalnie, dla każdej liczby rzeczywistej x, |x| = x, jeśli x ≥ 0, oraz |x| = -x, jeśli x < 0. Zatem wartość bezwzględna zawsze zwraca wartość nieujemną.
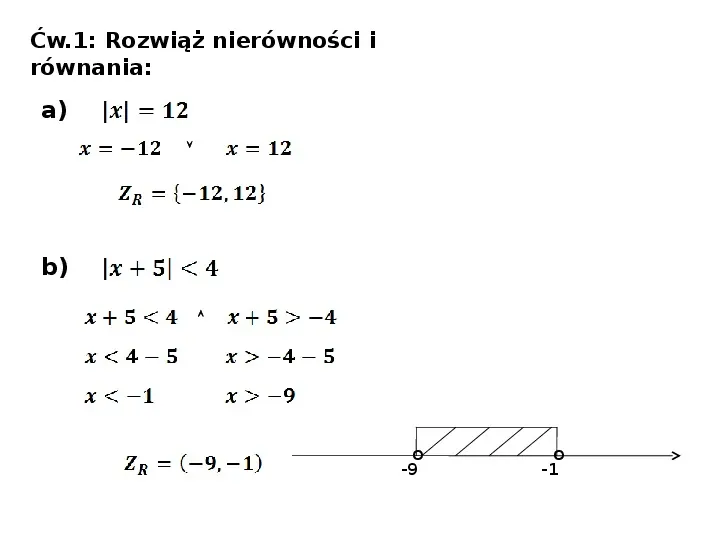
Rozwiązywanie równań z wartością bezwzględną sprowadza się do rozpatrzenia kilku przypadków, w zależności od znaku wyrażenia wewnątrz wartości bezwzględnej. Ogólna strategia polega na znalezieniu punktów zerowych wyrażenia wewnątrz modułu, a następnie rozważeniu oddzielnie przedziałów, w których to wyrażenie jest dodatnie lub ujemne. Dla każdego przedziału eliminujemy wartość bezwzględną, stosując odpowiednią definicję, a następnie rozwiązujemy otrzymane równanie liniowe lub kwadratowe. Ważne jest, aby na koniec sprawdzić, czy uzyskane rozwiązania należą do rozpatrywanego przedziału.
Podobnie, rozwiązując nierówności z wartością bezwzględną, wykorzystujemy rozbicie na przypadki. Kluczowe są dwie własności: |x| < a (gdzie a > 0) jest równoważne -a < x < a, natomiast |x| > a (gdzie a > 0) jest równoważne x < -a lub x > a. Przy bardziej złożonych nierównościach, zawierających wyrażenia algebraiczne wewnątrz modułu, należy postępować analogicznie jak w przypadku równań, rozważając przedziały i stosując odpowiednie własności, aby pozbyć się wartości bezwzględnej. Następnie, dla każdego przedziału rozwiązujemy nierówność i sprawdzamy, czy rozwiązania należą do tego przedziału. Ostatecznym rozwiązaniem jest suma (unia) rozwiązań uzyskanych dla każdego z przedziałów.
Praktyka w rozwiązywaniu zadań z wartością bezwzględną jest kluczowa dla opanowania tego zagadnienia. Zrozumienie definicji i własności wartości bezwzględnej, połączone z systematycznym rozważaniem przypadków i precyzyjnym rozwiązywaniem powstałych równań i nierówności, pozwala na skuteczne rozwiązywanie nawet bardziej złożonych problemów.