Rozważmy temat graniastosłupów w kontekście klasy 7 i materiałów typu Sprawdzian PDF. Co to wszystko oznacza?
Graniastosłup to bryła geometryczna, która ma dwie podstawy będące identycznymi wielokątami, połączone ścianami bocznymi, które są równoległobokami (najczęściej prostokątami). Graniastosłupy dzielimy na proste (ściany boczne prostopadłe do podstawy) i pochyłe, oraz na trójkątne, czworokątne, pięciokątne itd., w zależności od kształtu podstawy.
Klasa 7 w polskim systemie edukacji to rok, w którym uczniowie po raz pierwszy spotykają się z bardziej zaawansowanymi zagadnieniami geometrii przestrzennej, w tym z graniastosłupami. Obejmuje to rozpoznawanie, rysowanie, obliczanie pól powierzchni i objętości tych brył.
Sprawdzian PDF to format pliku, w którym udostępniane są testy, kartkówki i inne materiały kontrolne wiedzy. W kontekście graniastosłupów dla klasy 7, taki PDF zawiera zadania sprawdzające umiejętność obliczania pola powierzchni, objętości, rozpoznawania typów graniastosłupów oraz rozwiązywania zadań tekstowych związanych z tymi bryłami.
Takie materiały są pisane przez nauczycieli lub osoby przygotowujące pomoce dydaktyczne. Używane są przez nauczycieli do oceny wiedzy uczniów, a przez uczniów do nauki i przygotowania się do testów. Mają one kluczowe znaczenie w edukacji, ponieważ pozwalają na systematyczną kontrolę postępów w nauce i identyfikację obszarów wymagających dodatkowej pracy.
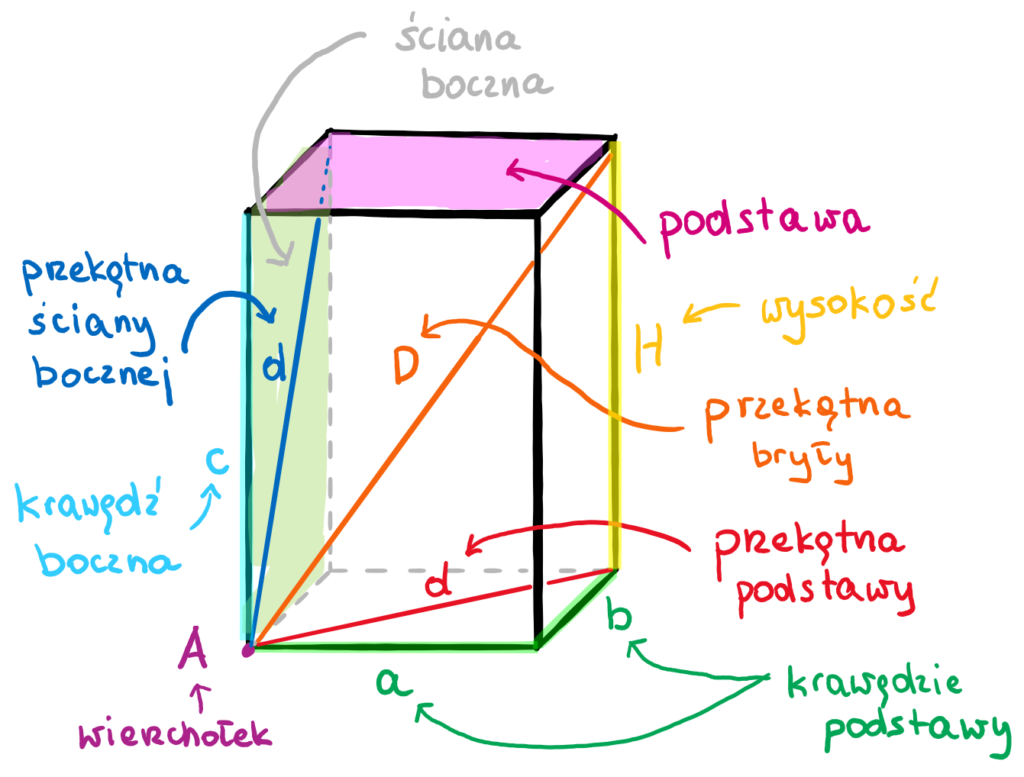
Znajomość graniastosłupów i umiejętność rozwiązywania zadań z nimi związanych jest istotna nie tylko w klasie 7, ale także w dalszej edukacji matematycznej i w wielu dziedzinach nauki i techniki.
Podsumowując, graniastosłupy stanowią ważny element nauki geometrii w klasie 7, a Sprawdziany PDF są użytecznym narzędziem do oceny i utrwalania wiedzy na ten temat. Odpowiednie zrozumienie i opanowanie tego materiału jest kluczowe dla dalszego rozwoju matematycznego ucznia.