Witaj! Przygotowujesz się do sprawdzianu z funkcji liniowej? Świetnie! Ten artykuł pomoże Ci zrozumieć kluczowe zagadnienia i rozwiązać typowe zadania.
Czym jest funkcja liniowa?
Funkcja liniowa to zależność między dwiema zmiennymi, którą można opisać wzorem: y = ax + b. x to zmienna niezależna (argument funkcji), a y to zmienna zależna (wartość funkcji). a i b to liczby, zwane współczynnikami.
Współczynnik a określa współczynnik kierunkowy. Informuje nas o nachyleniu prostej. Współczynnik b określa wyraz wolny. Mówi nam, w którym miejscu prosta przecina oś Y.
Przykład: y = 2x + 3. Tutaj a = 2, a b = 3. Oznacza to, że prosta jest rosnąca (bo a > 0) i przecina oś Y w punkcie (0, 3).
Rysowanie wykresu funkcji liniowej
Aby narysować wykres funkcji liniowej, potrzebujemy co najmniej dwóch punktów. Wybierz dwie dowolne wartości x i oblicz odpowiadające im wartości y. Następnie zaznacz te punkty na układzie współrzędnych i połącz je linią prostą.
Przykład: Dla funkcji y = -x + 1. Jeśli x = 0, to y = 1. Mamy punkt (0, 1). Jeśli x = 1, to y = 0. Mamy punkt (1, 0). Łączymy te punkty i mamy wykres.
Miejsca zerowe funkcji liniowej
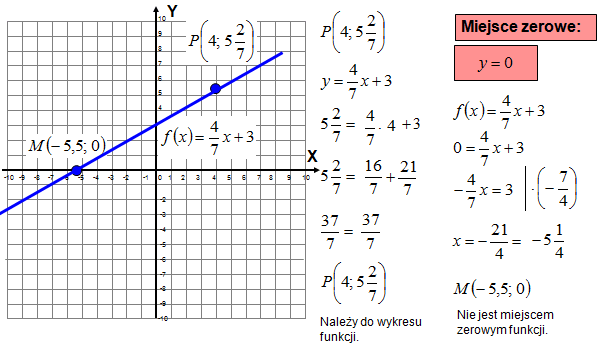
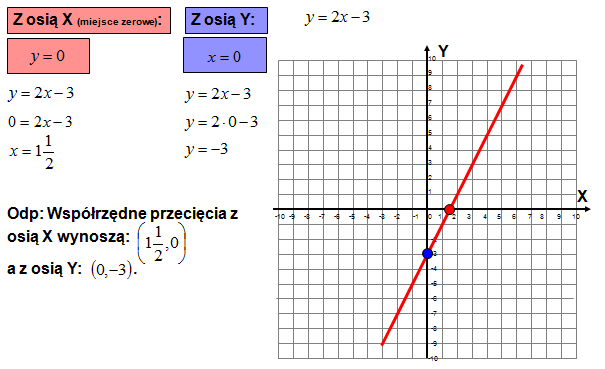
Miejsce zerowe funkcji to wartość x, dla której y = 0. Innymi słowy, to punkt, w którym wykres funkcji przecina oś X. Aby znaleźć miejsce zerowe, rozwiązujemy równanie ax + b = 0.

Przykład: Dla funkcji y = 3x - 6. Rozwiązujemy równanie 3x - 6 = 0. Dodajemy 6 do obu stron: 3x = 6. Dzielimy przez 3: x = 2. Miejsce zerowe to x = 2.
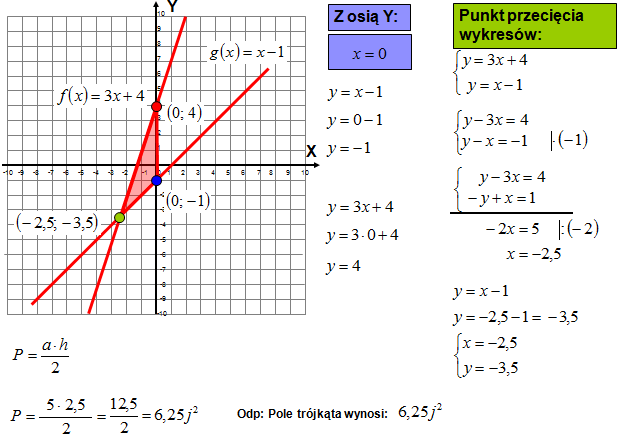
Równoległość i prostopadłość prostych
Dwie proste są równoległe, jeśli mają takie same współczynniki kierunkowe (a). Mają postać: y = ax + b1 i y = ax + b2. Proste są prostopadłe, jeśli iloczyn ich współczynników kierunkowych wynosi -1. Mają postać: y = ax + b1 i y = (-1/a)x + b2.
Przykład: Proste y = 2x + 1 i y = 2x - 3 są równoległe. Proste y = 2x + 1 i y = (-1/2)x + 5 są prostopadłe.
Rozwiązywanie zadań
Na sprawdzianie możesz spotkać zadania, w których będziesz musiał/a wyznaczyć wzór funkcji liniowej na podstawie danych punktów, znaleźć punkt przecięcia dwóch prostych, określić, czy proste są równoległe lub prostopadłe, narysować wykres funkcji, obliczyć miejsce zerowe.
Pamiętaj o dokładnym czytaniu poleceń i sprawdzaniu swoich obliczeń. Powodzenia na sprawdzianie!