
Funkcja kwadratowa to funkcja postaci f(x) = ax2 + bx + c, gdzie a, b, c są liczbami, a a jest różne od zera. Najważniejsze: musi być x2!
Co oznaczają a, b, c? 'a' mówi nam o kierunku paraboli. Jeśli a > 0, parabola ma ramiona skierowane do góry (uśmiech). Jeśli a < 0, ramiona są skierowane w dół (smutek). 'c' to punkt przecięcia z osią Y. Na przykład, w funkcji f(x) = 2x2 + 3x + 5, c = 5, więc wykres przecina oś Y w punkcie (0, 5).
Miejsca zerowe to wartości x, dla których f(x) = 0. Czyli, gdzie wykres funkcji przecina oś X. Aby je znaleźć, rozwiązujemy równanie kwadratowe ax2 + bx + c = 0. Używamy do tego delty (Δ), obliczanej ze wzoru: Δ = b2 - 4ac.
Jeśli Δ > 0, funkcja ma dwa miejsca zerowe. Jeśli Δ = 0, funkcja ma jedno miejsce zerowe. Jeśli Δ < 0, funkcja nie ma miejsc zerowych (wykres nie przecina osi X).
Wierzchołek paraboli to najważniejszy punkt na wykresie. Jego współrzędne to (p, q). p (współrzędna x) obliczamy ze wzoru p = -b / 2a. q (współrzędna y) obliczamy podstawiając p do wzoru funkcji, czyli q = f(p). Wierzchołek to minimum funkcji, gdy a > 0, i maksimum funkcji, gdy a < 0.
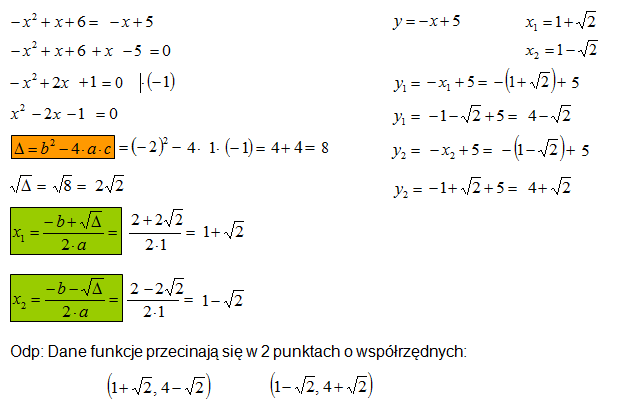
Postacie funkcji kwadratowej:
- Ogólna: f(x) = ax2 + bx + c
- Kanoniczna: f(x) = a(x - p)2 + q (p i q to współrzędne wierzchołka)
- Iloczynowa: f(x) = a(x - x1)(x - x2) (x1 i x2 to miejsca zerowe) - istnieje tylko, gdy Δ ≥ 0
Zrozumienie tych podstaw jest kluczowe do rozwiązywania zadań ze sprawdzianu z funkcji kwadratowej w liceum. Ćwicz obliczanie delty, wierzchołka i przekształcanie między postaciami funkcji.