
Potęgi i pierwiastki są fundamentalnymi operacjami matematycznymi, często sprawdzanymi na sprawdzianach GWO. Potęgowanie oznacza mnożenie liczby przez samą siebie określoną liczbę razy. Pierwiastkowanie to operacja odwrotna, czyli szukanie liczby, która pomnożona przez samą siebie (określoną liczbę razy) daje zadaną liczbę. Znajomość tych operacji jest kluczowa nie tylko do zdania sprawdzianu, ale także do zrozumienia bardziej zaawansowanych koncepcji matematycznych, fizycznych i informatycznych.
Praktyczne zastosowania:
- Potęgi: obliczanie powierzchni i objętości, modelowanie wzrostu populacji, informatyka (system binarny).
- Pierwiastki: obliczanie boków kwadratów i sześcianów, fizyka (prędkość, energia), statystyka.
Jak szybko rozwiązywać zadania z potęgami i pierwiastkami?
Krok 1: Potęgowanie
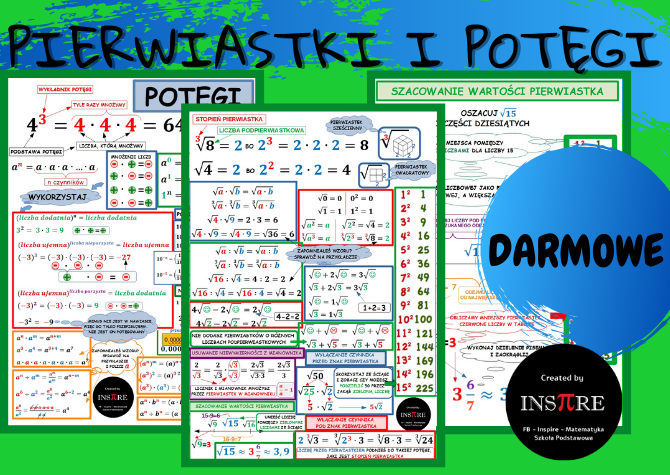
- Definicja: an = a * a * ... * a (n razy)
- Przykład: 23 = 2 * 2 * 2 = 8
- Pamiętaj: a0 = 1 (dla a ≠ 0), a1 = a
- Działania na potęgach: an * am = an+m, an / am = an-m, (an)m = an*m
Krok 2: Pierwiastkowanie
- Definicja: √[n]{a} = b, jeśli bn = a
- Przykład: √[2]{9} = 3 (ponieważ 32 = 9) - pierwiastek kwadratowy. √[3]{8} = 2 (ponieważ 23 = 8) - pierwiastek sześcienny.
- Pamiętaj: Pierwiastek kwadratowy z liczby ujemnej nie istnieje (w liczbach rzeczywistych).
- Upraszczanie pierwiastków: √{a * b} = √{a} * √{b}
Krok 3: Przykładowe zadanie i rozwiązanie

Oblicz: (32 + √[2]{16}) / 5
- Rozwiązanie:
- 32 = 9
- √[2]{16} = 4
- (9 + 4) / 5 = 13 / 5 = 2.6
Podsumowanie: Regularna praktyka z różnymi typami zadań to klucz do sukcesu na sprawdzianie GWO. Zrozumienie definicji i własności potęg i pierwiastków pozwoli na szybkie i efektywne rozwiązywanie problemów.