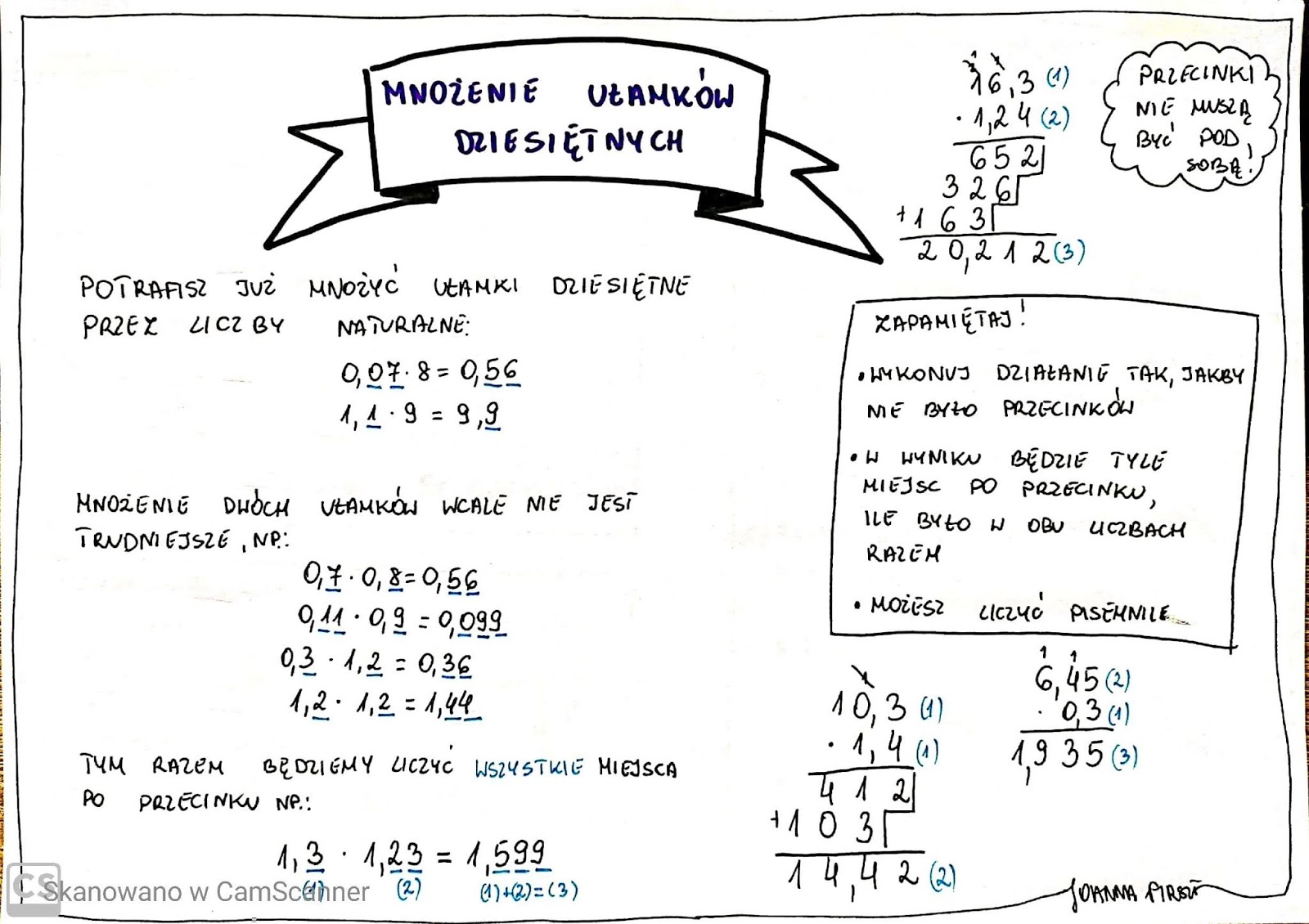
Mnożenie ułamków dziesiętnych w pamięci może wydawać się trudne, ale z odpowiednią strategią staje się prostsze. Kluczem jest rozłożenie problemu na mniejsze, łatwiejsze do zarządzania kroki. Skupimy się na kilku przydatnych technikach.
Usuń przecinki
Pierwszym krokiem jest pozbycie się przecinków dziesiętnych. Wyobraź sobie, że mnożysz liczby całkowite, a nie ułamki. Zapisz liczby bez przecinków. Na przykład, jeśli masz pomnożyć 0,25 przez 0,3, zapisz to jako 25 razy 3.
Wykonaj mnożenie liczb całkowitych
Teraz wykonaj mnożenie jak dla zwykłych liczb całkowitych. W naszym przykładzie, 25 razy 3 daje 75. Jest to prosty etap, który zwykle można łatwo wykonać w pamięci lub z pomocą szybkiego zapisu.
Dodaj przecinek z powrotem
To najważniejszy krok! Teraz musimy umieścić przecinek z powrotem we właściwym miejscu. Policz, ile miejsc po przecinku było w obu pierwotnych liczbach razem. W 0,25 mamy dwa miejsca po przecinku, a w 0,3 mamy jedno miejsce po przecinku. Razem daje to trzy miejsca po przecinku.
Umieść przecinek
Wróć do wyniku mnożenia liczb całkowitych, czyli 75. Musimy wstawić przecinek tak, aby mieć trzy miejsca po przecinku. Liczymy od prawej strony: 1, 2, a potrzebujemy trzeciego miejsca. Zatem musimy dodać zero z przodu, aby otrzymać 075. Teraz wstawiamy przecinek przed tym zerem. Otrzymujemy 0,075. Zatem 0,25 razy 0,3 to 0,075.

Przykład: 1,2 x 0,4
Spróbujmy innego przykładu: 1,2 razy 0,4. Usuwamy przecinki: 12 razy 4. Wykonujemy mnożenie: 12 razy 4 daje 48. Liczymy miejsca po przecinku w pierwotnych liczbach: 1,2 ma jedno miejsce, 0,4 ma jedno miejsce. Razem to dwa miejsca. Wstawiamy przecinek w 48, licząc od prawej: otrzymujemy 0,48. Zatem 1,2 razy 0,4 to 0,48.
Skracanie liczb
Czasami możesz uprościć obliczenia, zaokrąglając liczby. Pamiętaj jednak, że robisz to kosztem dokładności. To przydatne, gdy potrzebujesz szybkiego przybliżonego wyniku. Na przykład, mnożąc 1,98 przez 2,03, możesz zaokrąglić do 2 razy 2, co daje 4. Wynik będzie bliski rzeczywistemu.

Praktyka czyni mistrza
Najlepszym sposobem na opanowanie mnożenia ułamków dziesiętnych w pamięci jest ćwiczenie. Zacznij od prostych przykładów i stopniowo przechodź do bardziej skomplikowanych. Regularne ćwiczenia pozwolą Ci nabrać pewności siebie i wykonywać obliczenia szybciej i dokładniej.
Praktyczne zastosowania
Umiejętność mnożenia ułamków dziesiętnych w pamięci przydaje się w wielu sytuacjach. Na przykład, podczas zakupów, obliczania rabatów, dzielenia rachunków ze znajomymi czy planowania budżetu. To praktyczna umiejętność, która ułatwia codzienne życie.